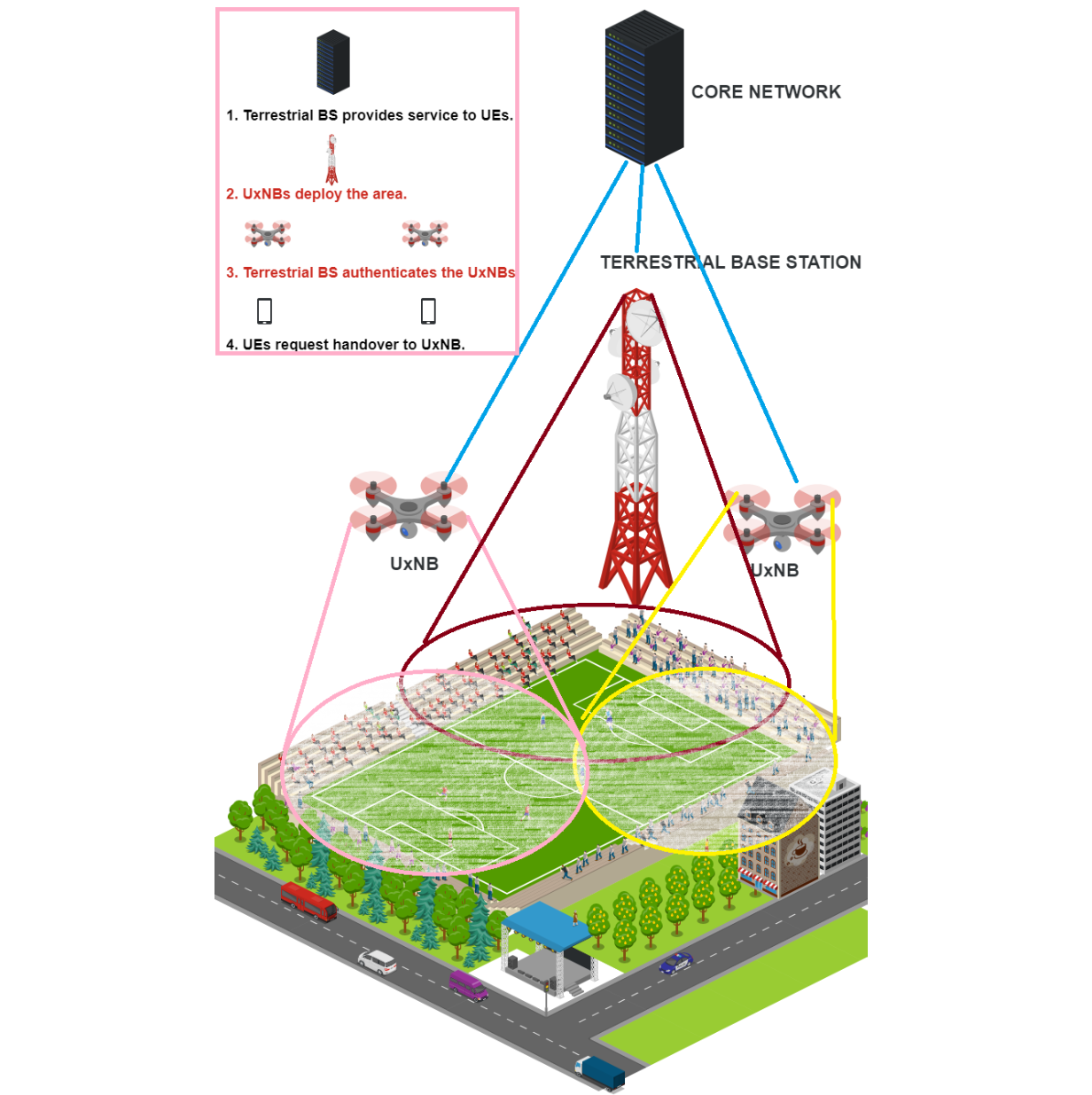
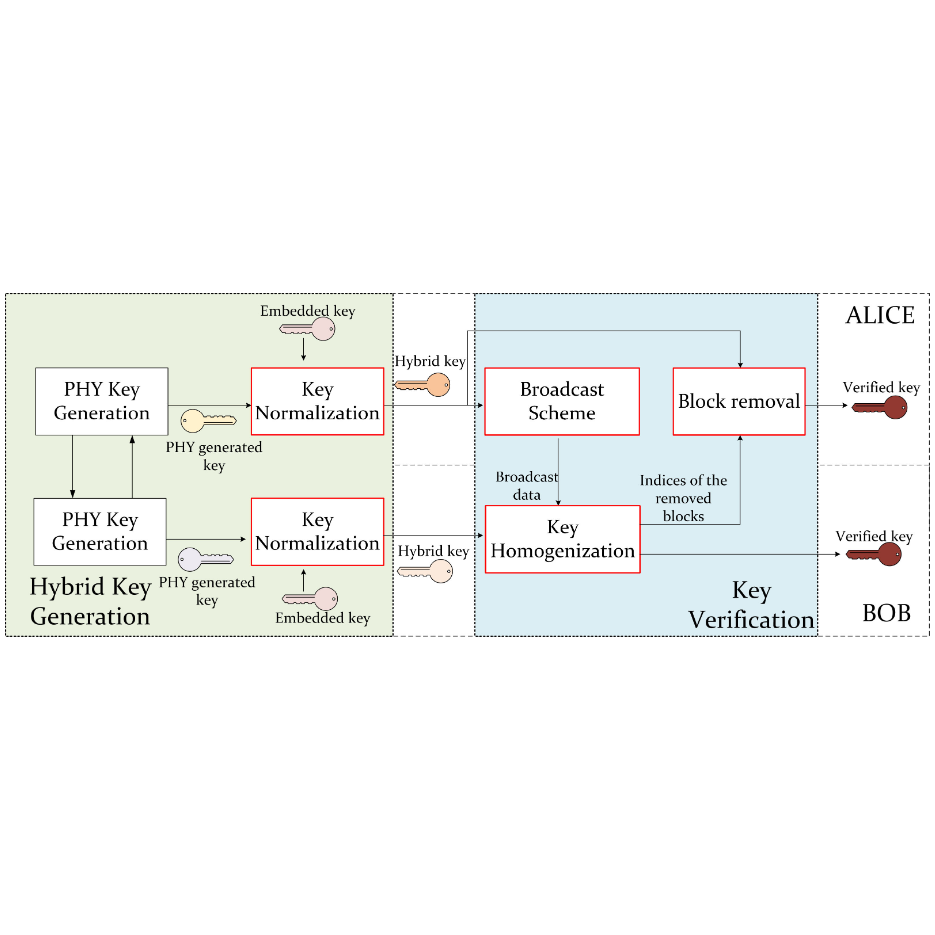
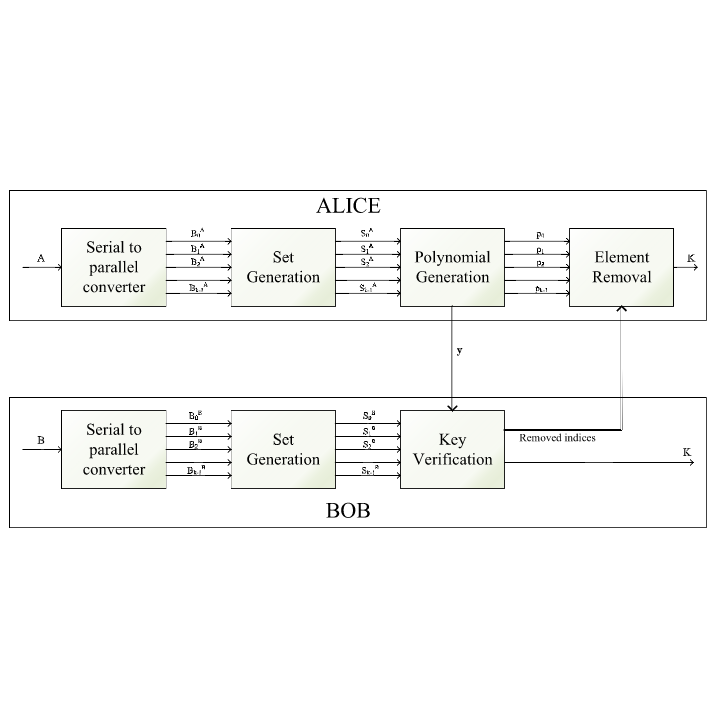
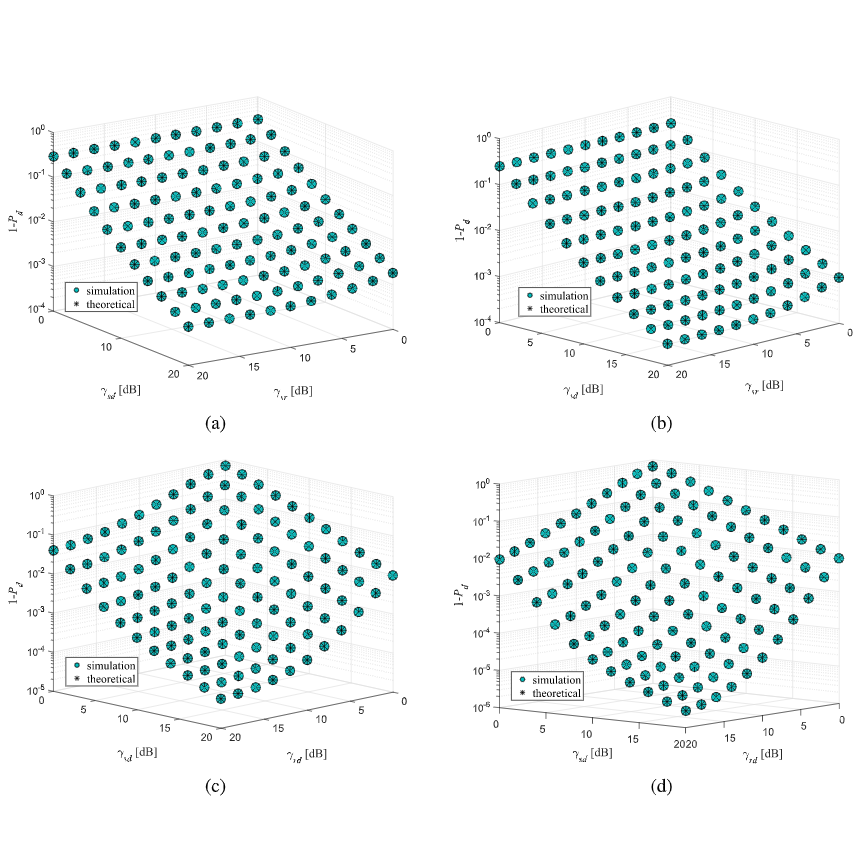
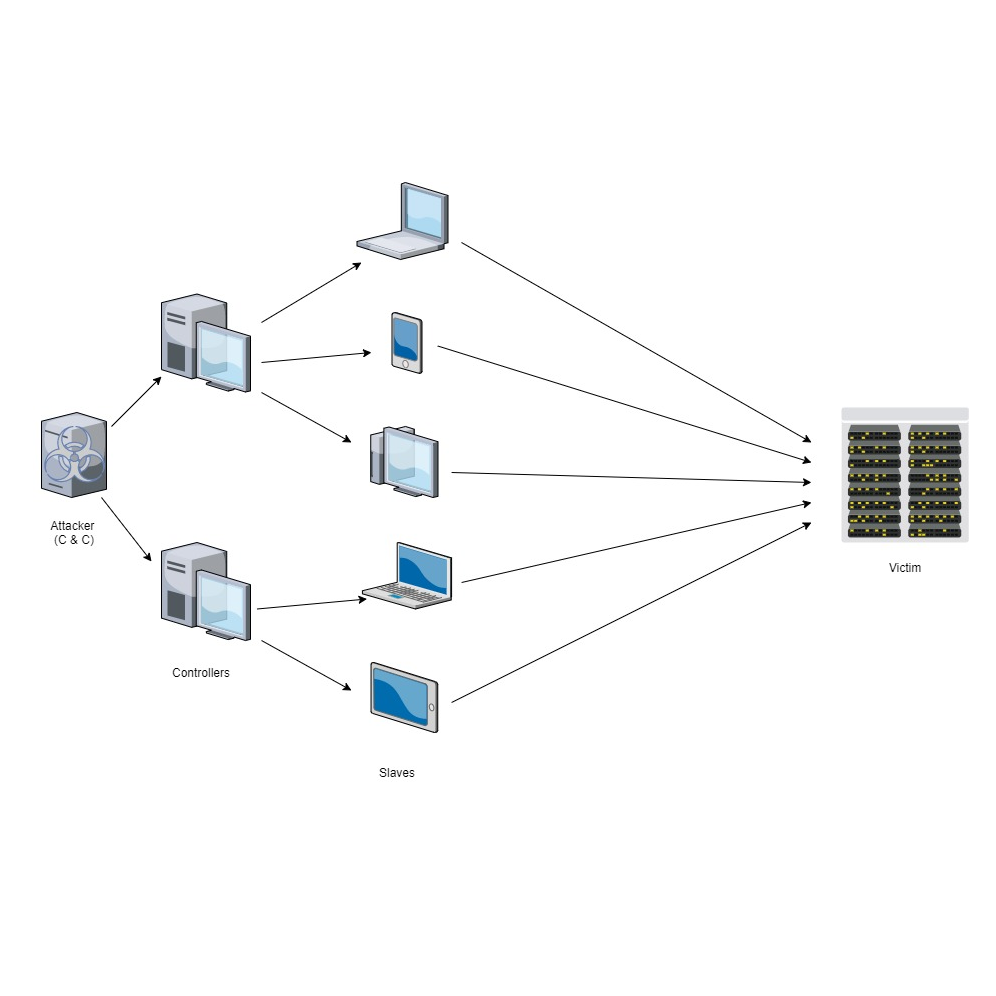
Privacy-Preseving Methods on IoVs
New authentication scheme
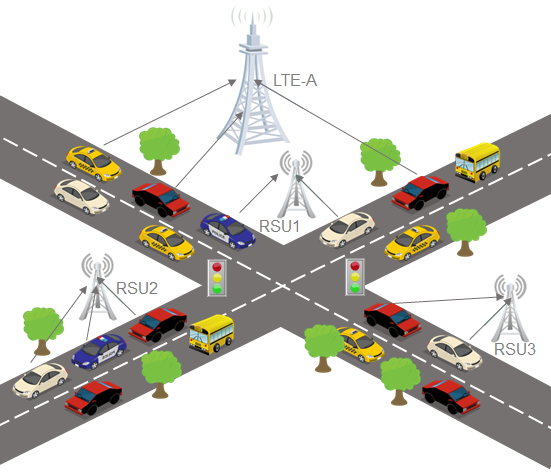
Phasellus quam turpis, feugiat sit amet ornare in, a hendrerit in lectus. Praesent semper mod quis eget mi. Etiam sed ante risus aliquam erat et volutpat. Praesent a dapibus velit. Curabitur sed nisi nunc, accumsan vestibulum lectus. Lorem ipsum dolor sit non aliquet sed, tempor et dolor. Praesent a dapibus velit. Curabitur accumsan.
Continue Reading